Breaches
3Di can simulate the consequences of a breach in a levee. In such case, the dimensions of the breach determine flow through the breach and therefore the flood. The growth of a breach is a very complex process. It is a phenomenon where hydrodynamics, morphology, groundwater and soil mechanics interact. Many aspects of this interaction is still unknown, and therefore it is difficult to model. Moreover, detailed modeling would require very detailed information about the levee. Generally, there is only a limited amount of information about the soil, structure, moisture content etc of the levee. Nevertheless, rules of thumb have been developed that describe the breach growth, which allow us to make an estimate of the breach growth.
In a 3Di model, flow may occur between 1D and 2D elements. In certain cases this exchange is limited by a levee. The exchange height is determined by the height of the levee. When a few extra properties of the levee are specified for these connections, a breach can be modelled that can grow over time. More information on levees, can be found in Obstacles
If you would like to know how to build a model with breaches, follow Tutorial 4: Building a dike breach flood model.
Breach growth formulation
In 3Di, the formula of Verheij and van de Knaap (2002) is used to describe the growth of a breach. For this formulation it is expected that the material of the levee (sand or clay), an initial breach width, the maximum breach depth and the period that is needed to reach this depth are known.
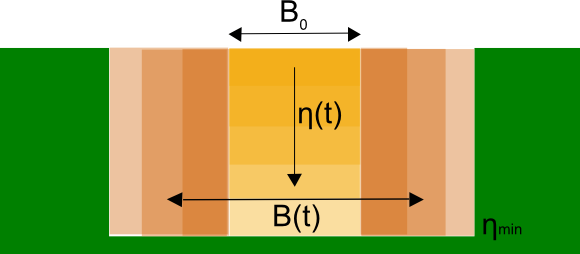
Fig. 39 Longitudinal cross-section of breach showing the breach growth parameters.
This formulation splits the growth of the breach into two phases; in the first phase the breach deepens and in the second phase the breach widens. Mathematically, the first phase can be described as:
Once the minimum breach level is reached, the width of the breach increases according to:
Parameter |
Clay |
Sand |
|---|---|---|
\(f_1\) |
0.8 |
0.02 |
\(f_2\) |
1.4 |
0.6 |
Because the water level gradient in front and behind the breach is included in the formulation, a natural balance may arise. This means that the breach stops growing, when the water levels are equal.
The above formulation also corrects for the presence of different types of materials by using a critical velocity and the parameters \(f_1\) and \(f_2\) . The growth rate of the breach increases for materials that erode more easily. In principle, this formulation distinguishes only sand and clay.
Breach flow
3Di uses a broad-crested weir formulation for the flow rate through a breach. The figure below shows the main variables and the three flow domains used in these equations.
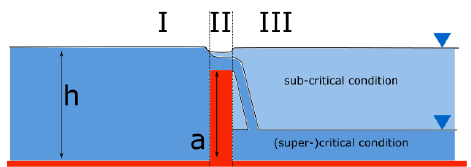
Water flows from domain I to III. When the breach opens, domain I will be the river or sea water level; later in the event, the river or sea level may fall so low that the flow direction reverses, and the flooded area will become upstream (domain I).
Which equation applies, depends on whether the flow is subcritical or (super)critical. The flow is (super)critical if the difference in water levels between domain I and III is greater than one-third of the water depth at the crest:
Supercritical breach flow
For supercritical flow the following equation applies:
In which:
For \(g\), 9.81 \(m/s^2\) is used; for \(L\), the fixed value of 30 m is used for breaches, representative for most dikes. The friction loss term \(\gamma\) is calculated as follows:
In which:
Subcritical breach flow
When the flow is subcritical, the following equation applies:
The variables used in this equation are identical to the variables used in the supercritical formulation and the \(\gamma\) is calculated following the same equations as in the previous section.